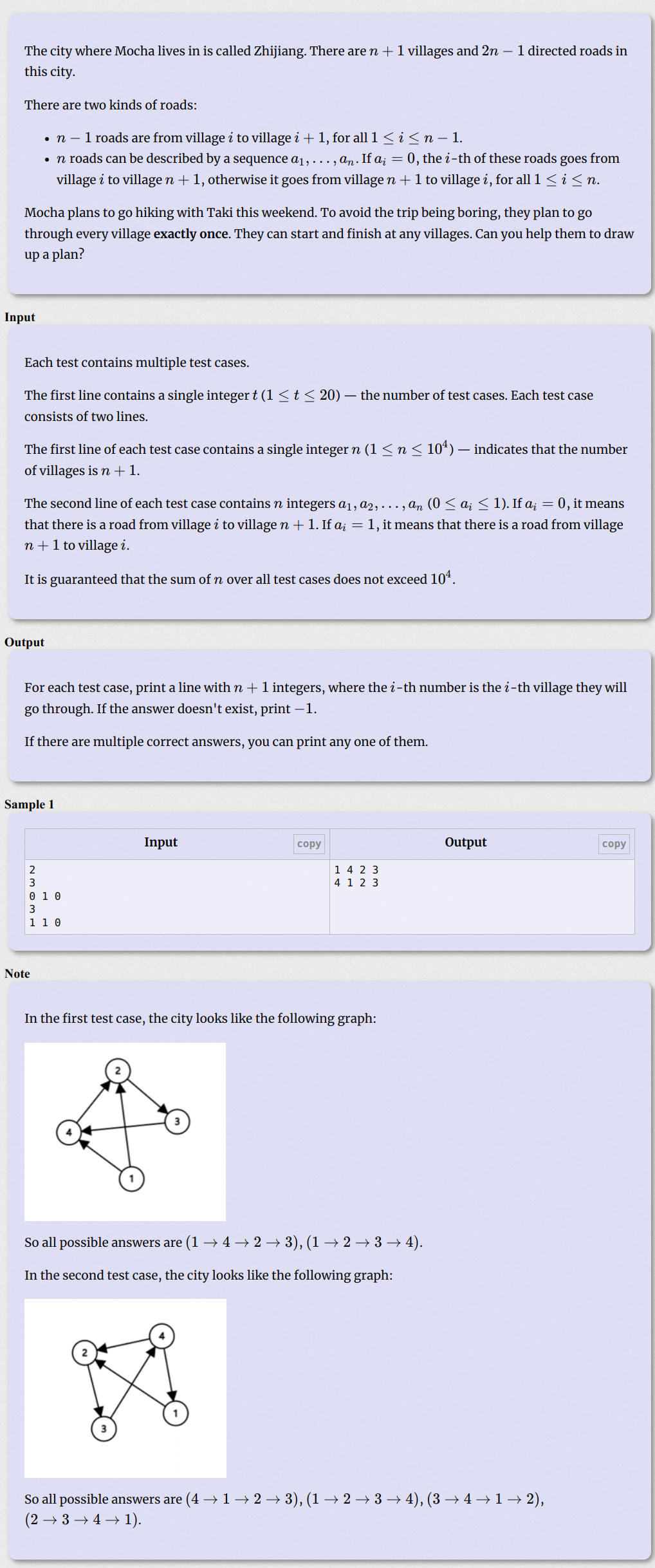
First consider vertex $n+1$, which can only visit once, meaning at most one $i\rightarrow n+1$ and at most one $n+1\rightarrow i$.
Then, there only three cases:
- $…\rightarrow i\rightarrow n+1\rightarrow i+1\rightarrow…$
- $…\rightarrow n\rightarrow n+1$
- $n+1\rightarrow1\rightarrow…$
// compile: make data
// run: ./data < data.in
#include <bits/stdc++.h>
using namespace std;
#pragma GCC optimize("O3,unroll-loops")
#pragma GCC target("avx2,bmi,bmi2,lzcnt,popcnt")
#ifdef LOCAL
#include <debug/codeforces.h>
#define debug(x...) _debug_print(#x, x);
#define Debug(x...) _debug_print_format(#x, x);
std::ifstream terminal("/dev/tty");
#define PP cerr<<"\033[1;30mpause...\e[0m",terminal.ignore();
#else
#define debug(x...)
#define Debug(x...)
#define PP
#endif
template<typename...Args> void print_(Args...args){((cout<<args<<" "),...)<<endl;}
#define rep(i,a,b) for(int i=(a);i<(int)(b);++i)
#define sz(v) ((int)(v).size())
#define print(...) print_(__VA_ARGS__);
#define FIND(a, x) ((find(a.begin(),a.end(),(x))!=a.end())?1:0)
#define cmin(x,...) x=min({(x),__VA_ARGS__})
#define cmax(x,...) x=max({(x),__VA_ARGS__})
#define INTMAX (int)(9223372036854775807)
#define INF (int)(1152921504606846976)
#define NaN (int)(0x8b88e1d0595d51d1)
#define double long double
#define int long long
#define uint unsigned long long
#define MAXN 200010
void solve() {
int n; cin >> n;
vector<int> a(n);
rep(i, 0, n) cin >> a[i];
if (a[n-1] == 0) {
rep(i, 0, n+1) cout << i+1 << " ";
cout << endl;
return;
}
if (a[0] == 1) {
cout << n+1;
rep(i, 0, n) cout << " " << i+1;
cout << endl;
return;
}
rep(i, 0, n-1) {
if (a[i] == 0 && a[i+1] == 1) {
rep(j, 0, i+1) cout << j+1 << " ";
cout << n+1;
rep(j, i+1, n) cout << " " << j+1;
cout << endl;
return;
}
}
cout << -1 << endl;
}
int32_t main() {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
int _; cin >> _;
while (_--) solve();
return 0;
}
Hey all, just wanted to drop a line about ae888land. Been having some good luck on their live casino games. Give them a spin! You can find them here: ae888land
Yo! I stumbled upon GK888win the other day. Pretty solid selection of games and the payouts seem fair. I recommend giving it a look-see. gk888win
Demopgslot é top pra quem quer treinar antes de apostar de verdade! Dá pra testar os jogos sem gastar nada. Ótima dica pra iniciantes! 😉 demopgslot
Baccarat strategy is fascinating – understanding patterns can help, but it’s never a guarantee! Seeing platforms like legend link ph legit embrace local payment options like GCash is smart for Filipino players, enhancing the experience. It’s all about responsible fun!
Really interesting read! It’s smart to see platforms like kkkkph777 vip focusing on responsible gaming and player well-being. A psychologically optimized environment sounds like a game-changer for enjoyment! 🤔
This Hamiltonian path approach is fascinating! The vertex n+1 constraint creates elegant case analysis that reminds me of game algorithm optimization. When designing slot mechanics at og777, we apply similar path-finding logic to ensure fair, deterministic outcomes while maintaining player engagement. Beautifully structured solution!
Pinatawinsbr, sounds Latin! Hopefully, the payouts are as sweet as a real piñata. Going to give it a bash see if I can get a win. Take a look at pinatawinsbr and see for yourself!
Sodocasinoearthgang, long name! Hope the slots are hotter than the Earth. Sounds like a fun theme. I might give it a whirl! Have a look at sodocasinoearthgang. Worth checking.
188betthethao – sounds like a solid sports betting platform. Hopefully, the odds are competitive. Fingers crossed! Try it if that sort of this is your bag 188betthethao and see, eh?